2D forced-dissipative turbulence

A simulation of forced-dissipative two-dimensional turbulence. We solve the two-dimensional vorticity equation with stochastic excitation and dissipation in the form of linear drag and hyperviscosity.

Install dependencies

First let's make sure we have all required packages installed.

using Pkg
pkg"add GeophysicalFlows, CUDA, CairoMakie"

Let's begin

Let's load GeophysicalFlows.jl and some other packages we need.

using GeophysicalFlows, CUDA, Random, Printf, CairoMakie

parsevalsum = FourierFlows.parsevalsum
record = CairoMakie.record                # disambiguate between CairoMakie.record and CUDA.record

Choosing a device: CPU or GPU

dev = CPU()     # Device (CPU/GPU)

Numerical, domain, and simulation parameters

First, we pick some numerical and physical parameters for our model.

 n, L  = 256, 2π             # grid resolution and domain length
 ν, nν = 2e-7, 2             # hyperviscosity coefficient and hyperviscosity order
 μ, nμ = 1e-1, 0             # linear drag coefficient
    dt = 0.005               # timestep
nsteps = 4000                # total number of steps
 nsubs = 20                  # number of steps between each plot

Forcing

We force the vorticity equation with stochastic excitation that is delta-correlated in time and while spatially homogeneously and isotropically correlated. The forcing has a spectrum with power in a ring in wavenumber space of radius $k_f$ (forcing_wavenumber) and width $δ_f$ (forcing_bandwidth), and it injects energy per unit area and per unit time equal to $\varepsilon$. That is, the forcing covariance spectrum is proportional to $\exp{[-(|\bm{k}| - k_f)^2 / (2 δ_f^2)]}$.

forcing_wavenumber = 14.0 * 2π/L  # the forcing wavenumber, `k_f`, for a spectrum that is a ring in wavenumber space
forcing_bandwidth  = 1.5  * 2π/L  # the width of the forcing spectrum, `δ_f`
ε = 0.1                           # energy input rate by the forcing

grid = TwoDGrid(dev; nx=n, Lx=L)

K = @. sqrt(grid.Krsq)             # a 2D array with the total wavenumber

forcing_spectrum = @. exp(-(K - forcing_wavenumber)^2 / (2 * forcing_bandwidth^2))
@CUDA.allowscalar forcing_spectrum[grid.Krsq .== 0] .= 0 # ensure forcing has zero domain-average

ε0 = parsevalsum(forcing_spectrum .* grid.invKrsq / 2, grid) / (grid.Lx * grid.Ly)
@. forcing_spectrum *= ε/ε0        # normalize forcing to inject energy at rate ε

We reset of the random number generator for reproducibility

if dev==CPU(); Random.seed!(1234); else; CUDA.seed!(1234); end

Next we construct function calcF! that computes a forcing realization every timestep. For that, we call randn! to obtain complex numbers whose real and imaginary part are normally-distributed with zero mean and variance 1/2.

function calcF!(Fh, sol, t, clock, vars, params, grid)
  randn!(Fh)
  @. Fh *= sqrt(forcing_spectrum) / sqrt(clock.dt)
  return nothing
end

Problem setup

We initialize a Problem by providing a set of keyword arguments. The stepper keyword defines the time-stepper to be used.

prob = TwoDNavierStokes.Problem(dev; nx=n, Lx=L, ν, nν, μ, nμ, dt, stepper="ETDRK4",
                                calcF=calcF!, stochastic=true)

Define some shortcuts for convenience.

sol, clock, vars, params, grid = prob.sol, prob.clock, prob.vars, prob.params, prob.grid

x, y = grid.x, grid.y

First let's see how a forcing realization looks like. Function calcF!() computes the forcing in Fourier space and saves it into variable vars.Fh, so we first need to go back to physical space.

Note that when plotting, we decorate the variable to be plotted with Array() to make sure it is brought back on the CPU when the variable lives on the GPU.

calcF!(vars.Fh, sol, 0.0, clock, vars, params, grid)

fig = Figure()

ax = Axis(fig[1, 1],
          xlabel = "x",
          ylabel = "y",
          aspect = 1,
          title = "a forcing realization",
          limits = ((-L/2, L/2), (-L/2, L/2)))

heatmap!(ax, x, y, Array(irfft(vars.Fh, grid.nx));
         colormap = :balance, colorrange = (-200, 200))

fig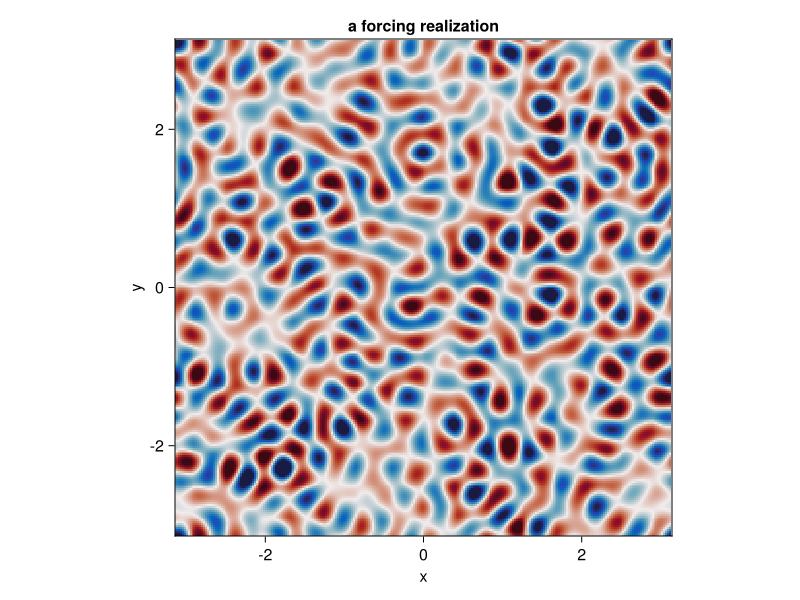

Setting initial conditions

Our initial condition is a fluid at rest.

TwoDNavierStokes.set_ζ!(prob, device_array(dev)(zeros(grid.nx, grid.ny)))

Diagnostics

Create Diagnostics; the diagnostics are aimed to probe the energy budget.

E  = Diagnostic(TwoDNavierStokes.energy,    prob; nsteps) # energy
Z  = Diagnostic(TwoDNavierStokes.enstrophy, prob; nsteps) # enstrophy
diags = [E, Z] # a list of Diagnostics passed to `stepforward!` will  be updated every timestep.

Visualizing the simulation

We initialize a plot with the vorticity field and the time-series of energy and enstrophy diagnostics. To plot energy and enstrophy on the same axes we scale enstrophy with $k_f^2$.

ζ = Observable(Array(vars.ζ))
title_ζ = Observable("vorticity, μ t=" * @sprintf("%.2f", μ * clock.t))

energy = Observable(Point2f[(μ * E.t[1], E.data[1])])
enstrophy = Observable(Point2f[(μ * Z.t[1], Z.data[1] / forcing_wavenumber^2)])

fig = Figure(resolution = (800, 360))

axζ = Axis(fig[1, 1];
           xlabel = "x",
           ylabel = "y",
           title = title_ζ,
           aspect = 1,
           limits = ((-L/2, L/2), (-L/2, L/2)))

ax2 = Axis(fig[1, 2],
           xlabel = "μ t",
           limits = ((0, 1.1 * μ * nsteps * dt), (0, 0.55)))

heatmap!(axζ, x, y, ζ;
         colormap = :balance, colorrange = (-40, 40))

hE = lines!(ax2, energy; linewidth = 3)
hZ = lines!(ax2, enstrophy; linewidth = 3, color = :red)
Legend(fig[1, 3], [hE, hZ], ["energy E(t)", "enstrophy Z(t) / k_f²"])

fig

Time-stepping the Problem forward

We step the Problem forward in time.

startwalltime = time()

record(fig, "twodturb_forced.mp4", 0:round(Int, nsteps / nsubs), framerate = 18) do j
  if j % (1000/nsubs) == 0
    cfl = clock.dt * maximum([maximum(vars.u) / grid.dx, maximum(vars.v) / grid.dy])

    log = @sprintf("step: %04d, t: %d, cfl: %.2f, E: %.4f, Z: %.4f, walltime: %.2f min",
          clock.step, clock.t, cfl, E.data[E.i], Z.data[Z.i], (time()-startwalltime)/60)
    println(log)
  end

  ζ[] = vars.ζ

  energy[] = push!(energy[], Point2f(μ * E.t[E.i], E.data[E.i]))
  enstrophy[] = push!(enstrophy[], Point2f(μ * Z.t[E.i], Z.data[Z.i] / forcing_wavenumber^2))

  title_ζ[] = "vorticity, μ t=" * @sprintf("%.2f", μ * clock.t)

  stepforward!(prob, diags, nsubs)
  TwoDNavierStokes.updatevars!(prob)
end

step: 0000, t: 0, cfl: 0.00, E: 0.0000, Z: 0.0000, walltime: 0.00 min
step: 1000, t: 5, cfl: 0.43, E: 0.2881, Z: 34.9014, walltime: 0.14 min
step: 2000, t: 10, cfl: 0.53, E: 0.3803, Z: 33.7438, walltime: 0.23 min
step: 3000, t: 15, cfl: 0.48, E: 0.4326, Z: 36.7366, walltime: 0.33 min
step: 4000, t: 20, cfl: 0.53, E: 0.4520, Z: 34.9454, walltime: 0.43 min

This page was generated using Literate.jl.